Последовательность Фибоначчи: что это такое простыми словами, где применяется и как определяется

Человечество на протяжении многих тысяч лет сталкивалось с различными закономерностями в окружающем их мире. По мере развития науки люди начали описывать многие вещи с помощью математических инструментов. Создание моделей позволяет понять суть различных процессов, а также создает возможность прогнозирования. Один из таких способов – последовательность Фибоначчи.

Как Леонардо Фибоначчи изобрел свою известную последовательность

Леонардо Пизано по прозвищу Фибоначчи – европейский математик 12 в. Родом из Пизы, он по воле отца направился для изучения математики и торгового дела в Алжир к арабским учителям.

Фибоначчи открыл свою известную последовательность, когда задался вопросом о разведении кроликов. Суть задачи: «Пару кроликов заселяют на поляну. Сколько пар будет жить на этом месте через год?». Для решения были введены упрощения: кролики в течение года не умирают, половой зрелости достигают спустя месяц после рождения, потомки появляются только спустя месяц после зачатия.

Леонардо Фибоначчи

Таким образом, в этой задаче последовательность определяется так:

• первый месяц – 1 пара;
• второй месяц – 1+1=2 пары;
• третий месяц – 2+1=3 пары, тут рожает первая пара кроликов, так как вторая еще на третий месяц только достигла половой зрелости;
• четвертый месяц – 3+2=5 пар, здесь уже рожает и первая пара, и первые потомки, т.е. появляются на свет 2 пары.

В конце года на поляне будет 144+233=377 пар кроликов.

Что это и для чего нужно

Последовательность Фибоначчи простыми словами – это прогрессия, состоящая из целых чисел, следующих друг за другом с определенной закономерностью. Каждый последующий элемент равен сумме двух предыдущих.

Большой интерес представляет частное двух соседних чисел, для всех элементов ряда приблизительно равное цифре 1,618. Это значение получило название «золотое сечение». Именно оно лежит в основе натуральной гармонии нашей Вселенной, присущей галактикам, цветам, животным.

Последовательность чисел Фибоначчи

Так исторически сложилось, что первыми выявили и описали «золотое сечение» древнегреческие математики. Оно представляло собой деление отрезка АВ точкой С на части таким образом, что большая часть отрезка относится к меньшей, как весь отрезок к большей части: ВС/АС=АВ/ВС.

Позднее, в начале 13-го века, Фибоначчи привел обоснование и доказательства существования этой последовательности и «золотого сечения». В 19 веке теоретик Эдуард Люка дал название этой прогрессии — «последовательность Фибоначчи».

Где используют

Золотое сечение наряду с загадочными свойствами чисел Фибоначчи с далеких времен и по сей день привлекают внимание ученых. Область применения последовательности довольна широка. Это может быть искусство, архитектура. Например, правило встречается на полотне И. Левитана «Сумерки. Луна» с выстроенным центром (Луной), линией горизонта, темными акцентами по правилам золотого сечения в соотношении 1,618. Соответственно, здесь и будут расположены наиболее важные части экспозиции.

В архитектуре пример «золотых» линий — знаменитая пирамида Хеопса. В древнегреческих строениях универсальное правило можно проследить, изучая Парфенон. В те времена считалось, что объекты с именно таким соотношением частей наиболее приятны для глаз человека.

Применение в трейдинге

Первым человеком, кто решил заняться изучением рынков на основе применения последовательности чисел Фибоначчи, является Ральф Нельсон Эллиот. Будучи финансистом, он смог обнаружить и определенную закономерность в поведении фондовых рынков, также поддающихся правилу золотого сечения.

Применение последовательности Фибоначчи в трейдинге

Коррекции Фибоначчи

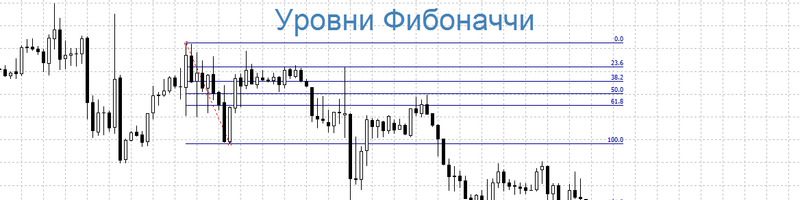
Коррекции, или уровни Фибоначчи – это инструмент технического анализа, служащий для прогнозирования уровней поддержки и сопротивления.

Для построения требуется произвести следующий порядок действий:

1. Определяют экстремумы (максимальное и минимальное значение) на графике в долгосрочном периоде.
2. На основе этих точек отстраивают вертикальный отрезок и делят на коэффициенты Фибоначчи, равные 23,6%, 38,2%, 50%, 61,8%.
3. На графике рисуют горизонтальные прямые, соответствующие полученным значениям. Эти линии представляют собой уровни поддержки, что означает окончание падения цены, и сопротивления – цена не идет выше.

Значения коэффициентов получают по следующей формуле, согласно числам Фибоначчи (0,1,1,2,3,5,8,13,21,34,55,89,144…):

• 23,6%. Получают путем деления одного члена последовательности на число, находящееся на 3 позиции впереди от него. Например: (34/144)·100=23,6%, т. е. в последовательности берется цифра 34 и делится на число, находящееся впереди на 3 шага – это 144. Чем дальше от нулевого значения, тем точнее будет коэффициент.
• 38,2%. Деление одного числа на то, что стоит двумя позициями дальше. Например: (34/89)·100=38,2%.
• 61,8%. Частное двух соседних членов последовательности. Например: (89/144)·100=61,8%.

Существуют еще 3 уровня, не входящих в соотношения Фибоначчи:

• 0%. Означает начало отката.
• 50%. Эмпирический коэффициент, которым пользуется большое количество трейдеров. Рынок имеет тенденцию к развороту при откате в 50%.
• 100%. Это разворот рынка в противоположную сторону.

Дуги Фибоначчи

Один из индикаторов, представляющий дуги, которые могут быть уровнями поддержки и сопротивления. Трейдеры при помощи этого инструмента имеют возможность прогнозировать моменты разворота рынка, чтоб своевременно зафиксировать прибыль.

Дуги Фибоначчи

Построение производят также на основе экстремумов графика. Определяют желаемую точку. Затем от нее на расстояниях 38,2%, 50% и 61,8% отстраивают дуги.

Тем самым можно определить уровни сопротивления и поддержки цены.

При растущем тренде с помощью дуг возможно понять, до какого значения опустится цена перед ее следующим подъемом. И, наоборот, при снижении цены акции дуги показывают, как может вырасти цена до ее следующего падения.

Веера Фибоначчи

Представляют диагональные линии, исходящие из одной точки. Формой походят на веер.

Для построения требуется произвести следующие действия;

1. Определить экстремумы на графике.
2. Из выбранной точки провести наклонную линию. Если тренд возрастающий, то прямую проводят до точки с наибольшим значением, если падающий – до точки минимума.
3. От второй точки мысленно отстраивают вертикальную прямую.
4. На этой линии выделяют уровни в 38,2%, 50% и 61,8%. Далее через эти точки проводят прямые. Эти линии будут показывать на области с потенциальной силой покупателей или продавцов.

Временные зоны Фибоначчи

Это инструмент технического анализа рынка, который представляет ряд вертикальных линий, построенных в рамках числовых значений Фибоначчи. Принцип работы основан на временных отрезках, а не на движении цен.

На графике отмечают явный ценовой тренд, основанный на точках экстремума. Горизонтальное расстояние между ними – единичный отрезок. Далее строят параллельные вертикальные линии. Эти прямые будут характеризовать временные зоны, в которых с некоторой долей вероятности можно ожидать падение или взлета цен. Первый уровень должен совпадать с пиковым значением тренда на графике. Но для большей уверенности желательно, чтоб и второй уровень приходился на экстремальное значение.

Похожие записи:

Торговля на Forex по стратегии Pivot Woodie CCI – описание торговой системы, индикаторы, паттерны, способы входа и выхода Восходящая линия тренда, пример правильного построения восходящей трендовой линии Форекс-стратегия «Соковыжималка»: суть, последовательность торговых операций и примеры